Why do I need lru_cache?

Often when running a function that takes a long time (due to either computational complexity or I/O latency), it's a good ideas to add memoization. That's a fancy word meaning "to save results".

If you're calling a function recursively, it's probably a good idea to cache the intermediate results to cut down on the runtime.

A bad function without lru_cache

Take the classic fibonacci equation. In Python it could look something like this:

def fib(n):
    if n <= 1:
        return n
    else:
        return fib(n-2) + fib(n-1)

Now let's time the function calls to see how it's growing over time.

import timeit

times = []

def func_time(n):
    return timeit.timeit('fib(%s)' % n, setup="from __main__ import fib", number=1)

for i in range(37):
    times.append(func_time(i))

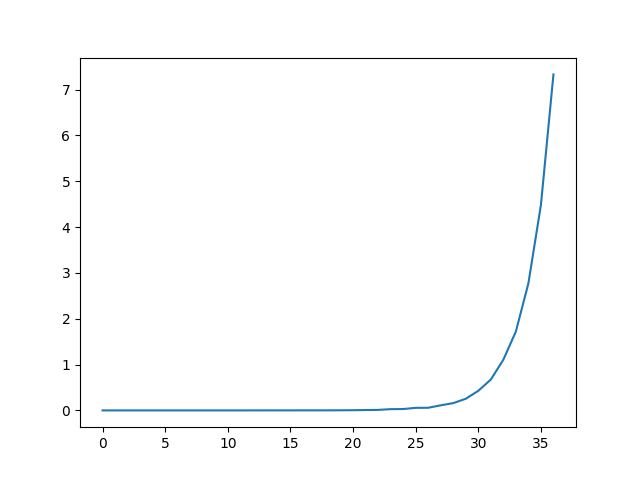
If we plot the graph of time for each function call it looks like this:

import pandas as pd
import matplotlib.pyplot as plt

pd.Series(times).plot()
plt.show()

This graph is growing on the order of O(2ⁿ). That means that for every additional call, it's going to take about double the amount before it. When the function calls are taking less than a second to run, it's hardly noticeable, but there's a big difference between waiting a few minutes and a few hours.

How can lru_cache fit in?

lru_cache is a decorator, so once the function is decorated, you're done! There's a parameter for how many values to store in the cache, so for our case of going through 37 values using range we want at least that amount in the cache.

from functools import lru_cache

@lru_cache(maxsize=128)
def fib(n):
    if n <= 1:
        return n
    else:
        return fib(n-2) + fib(n-1)

If we run the timeit section above, again, we get a graph that looks like this.

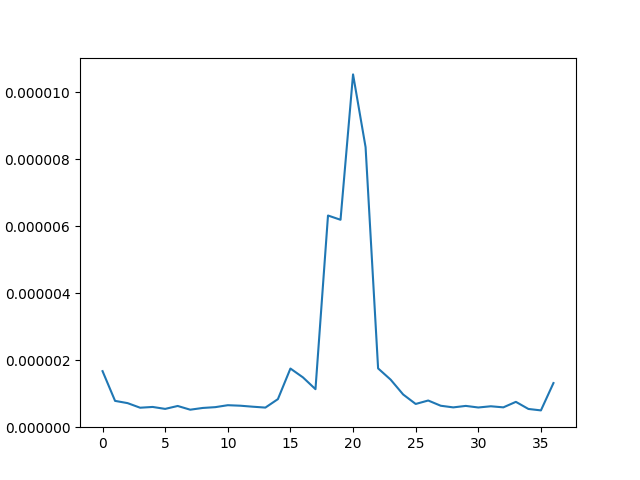
Besides the fact that it almost ran instantly, it's almost running in O(1) time, too.

We can even bump up the number to look for the 1000th fibonacci and it also runs just as quick. That timed graph looks like this.

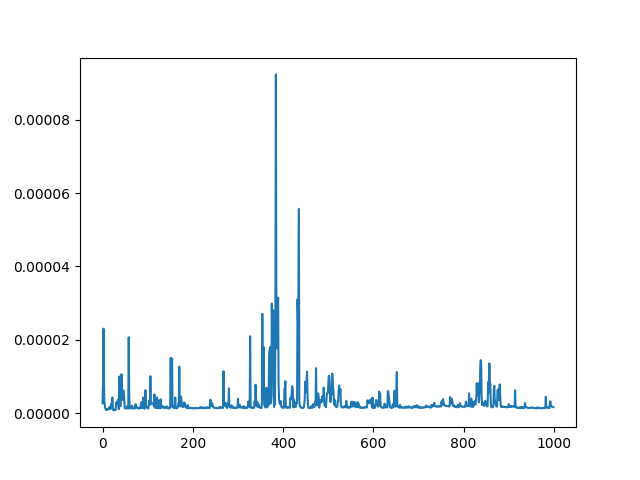
Why did this go so much faster?

The fibonnaci function runs in O(2ⁿ) time since every call has to make two calls to the previous fibonacci functions. That makes the number of calls double over time. If you're calling fib(10) you're going to be calling fib(1) 2¹⁰ times. When we cache the results using lru_cache we save the value of the intermediate calls, such as fib(3) and fib(4). Once we have those values, the value is returned and we don't need to continue making repeated recursive function calls.

Other uses

The example shows how lru_cache can aid with memoization to store intermediate recursive function calls. Another instance for using lru_cache would be if you have some long-running function call that returns some sort of data, such as a call to a database or an API. After the first run, which may take a few minutes, the second call to the function will be very quick.

Additonal parameters

There's a cache_info() method once lru_cache is called that shows information regarding the cache.

fib.cache_info()

>>> CacheInfo(hits=70, misses=37, maxsize=128, currsize=37)

• hits is number of times the cache was reused instead of calling the function, while misses is number of times it needed to run the function.

  • Since I ran fib 37 times, it makes sense that there would be at least 37 times where there would not be a value in the cache.

• maxsize and currsize are the max size of the cache and the current size of the cache, respectively.

  • From the lru_cache documentation, "If maxsize is set to None, the LRU feature is disabled and the cache can grow without bound. The LRU feature performs best when maxsize is a power-of-two."

• In lru_cache there's another parameter of typed which, if set to true will cache function arguments of different types separately

  • For example, fib(3) and fib(3.0) will be treated as distinct calls with distinct results.

What happens when the cache is full? The lru in lru_cache stands for "least recently used". Therefore, once the cache is full, the oldest values start to get thrown out.

Conclusion

The lru_cache decorator from the functools module is a very easy way to add caching to expensive functions. In this post you've seen how easy it is to cut down a function from O(2ⁿ) time to O(1) time using lru_cache and should be able to tell when a function might necessitate its use.